Centroid Decomposition of a Tree

Introduction : Centroid Decomposition is just a divide and conquer technique which is used on trees and turns out useful in many problems. It is also known as “Separator Decomposition”. In this article I will first explain How do we do centroid decomposition followed by it’s applications (i.e. Why do we do it ? ) . In the end, I will discuss a few problems that can be easily solved using centroid decomposition.
So, let’s begin 🙂

Pr-requisites : Basic graph theory. DFS . (Basic) Divide and Conquer.

What is Centroid and How to find it ?

Centroid of a Tree : Given a tree with N nodes, a centroid is a node whose removal splits the given tree into a forest of trees , where each of the resulting tree contains no more than N/2 nodes. (Do not confuse it with center of a tree. See this and this for more about center of a tree)  eg:

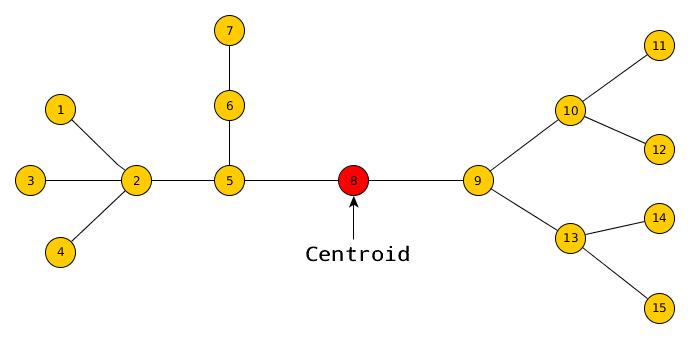
Theorem (Jordan, 1869) : Given a tree with N nodes,  there  exists a vertex whose  removal partitions the tree into components, each with at most N/2 nodes. (i.e. For any given tree, the centroid always exists)
Proof : Let us chose any arbitrary vertex v in the tree, if v satisfies the property of the centroid, then we are done, else there exists one (and only one) component with more than N/2 vertices. We now consider the vertex u adjacent to v in that component and apply the same argument for u . We continue the same procedure unless we find the required vertex. Also, we never go back to any old vertices because the component containing them must have less than N/2 vertices. Since the no of vertices are finite, and we visit each vertex at most once, the procedure must end and hence the centroid must exist.

Finding the centroid of a tree : One way to find the centroid is to pick an arbitrary root, then run a  depth-first search computing the size of each subtree, and then move  starting from root to the largest subtree until we reach a vertex where  no subtree has size greater than N/2. This vertex would be the centroid of the tree.

Decomposing the Tree to get the new “Centroid Tree” :

On removing the centroid, the original given tree decomposes into a number of different trees, each having no of nodes < N/2 . We make this centroid the root of our centroid tree and then recursively decompose each of the new trees formed and attach their centroids as children to our root. Thus , a new centroid tree is formed from the original tree. eg: For the following tree :

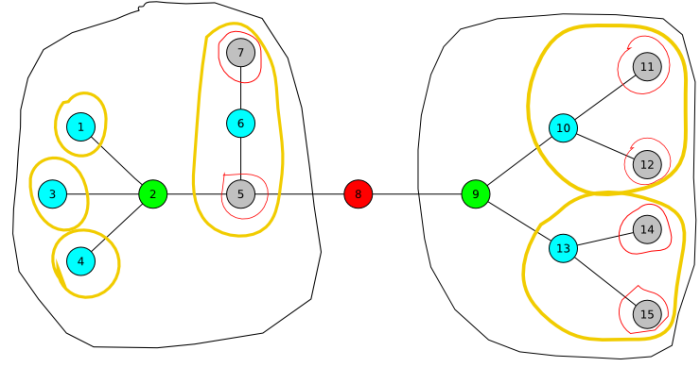
The Centroid Tree formed would be as follows :

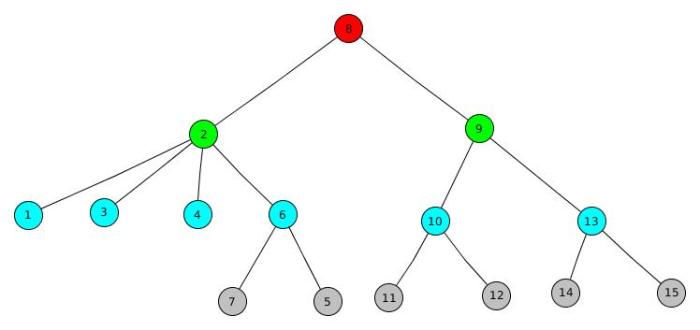
Properties of Centroid Tree :

1. The tree formed contains all the N nodes of the original tree. 
   • Since each node will become a centroid of some smaller tree (maybe a tree consisting only of that one single node) , Hence the centroid tree formed would contain all the N nodes of the original tree.
2. The height of the centroid tree is at most O(logN).
   • Since at each step, the new trees formed by removing the centroid have size at-most N/2, the maximum no of levels would be O(logN). Hence, the height of the centroid tree would be at most O(logN).
3. Consider any two arbitrary vertices A and B and the path between them (in the original tree) can be broken down into A–>C and C–>B where C is LCA of A and B in the centroid tree.
   • It is not hard to see that given any arbitrary vertices A and B and their LCA C in the centroid tree , both A and B lie inside the part which the vertex C was centroid of, and they were first separated into different parts when the vertex C was removed. (convince yourself from the diagram above before moving on).
   • The vertex C can also be seen as : If we assign labels to centroids in the order in which they are removed from the graph / labels equal to the level at which the centroid occurs in the centroid tree, then C would be the node with smallest label on the path from A–>B in the original tree. eg : In the diagram above, the labels would be given as follows :
     node numbers   node colour   label given
     8                       Red               0
     2 , 9                   Green             1
     1,3,4,6,10,13           Blue               2
     7,5,11,12,14,15        Grey              3
4. Hence, we decompose the given tree into O(NlogN) different paths (from each centroid to all the vertices in the corresponding part) such that any path is a concatenation of two different paths from this set. (This is the most important/new/extra part in this DS that should be focused on)
   • Using some DS , we maintain the required information (based on the problem) about these O(NlogN) different path chosen such that any other path can be decomposed into 2 different paths from this set and these two paths can be found in O(logN) time, by finding the LCA in the centroid tree (since height of centroid tree is at most O(logN), we can find the LCA by just moving up from the deeper node).

 

Problem Discussion :

The above decomposition turns out to be useful in many problems. I will discuss a few problems that can be efficiently solved using Centroid Decomposition to help get a better feel of the technique and its usage.

1. Problem – E – Codeforces
   • Let ans[i] denote the min distance to a red node for the centroid “i” in it’s corresponding part. Hence initially, let ans[i]=INF, for all i.
   • For each update , to paint a node u red, we move up to all the ancestors x of u in the centroid tree and update their ans as ,
     ans[x] = min(ans[x],dist(x,u))
     because node u will be in the part of all the ancestors of u.
   • For each query, to get the closest red node to node u, we again move up to all the ancestors of u in the centroid tree and take the minimum as  :
     mn = min(mn , dist(x,u) + ans[x] );
   • Why would this work ??
     Let x be the closest red node to u in the graph. If x lies in the part of u, dist(u,u) + ans[u] would give the minimum distance and all it’s ancestor’s would give a distance greater than this , hence the minimum would not be affected. Same argument would work if x lies in any one of the ancestors of u. Also, x must lie in the part of any one ancestor because the root node of centroid tree represents the whole tree.
   • Hence both update and query will be O(log^2N). (O(logN) to get distance between two nodes and O(logN) ancestors for each node. See this for implementation details)
   • To be more clear, try changing the query from “closest red node” to “farthest red node” and think whether the same argument would work for it or not.  🙂
2. SPOJ.com – Problem QTREE5
   • A very similar problem as above. The only difference is that now, we can even revert back to the original colour.
   • Hence we might maintain a multiset for each node instead of just one minimum distance and process the queries in a very similar way as above.
   • The complexity ?  O(log^2 N) (with an extra “additive” O(logN) factor per query/update because of the multiset)
   • An interesting observation/optimization to remove the extra additive O(logN) factor is that we only need distance between a node and all it’s ancestors in the centroid tree. Also, if we root a tree at it’s centroid, we can get distances from centroid to all other nodes in the tree. Hence, we maintain a “dist[LOGN][N]” array such that dist[i][j] is the distance of node j from the root in the i’th level of decomposition. Hence, now the distance of a node to it’s ancestor can be found in O(1) using the above information but building this dist array also means an extra additive O(n) at each O(logN) levels of decomposition.(The observation is important although it might not be as useful in this specific problem 🙂 )
3. Prime Distance On Tree :
   • We need to find the no of pairs of nodes, the distance between which is a prime no, and then divide this no by nC2 , to get the required answer.
   • For each centroid, we find the no of nodes at distance “i” from the centroid in it’s part and store it in dist[i].
   • We then remove the centroid and move to each part one by one which the centroid decomposes the tree into, and remove the contribution of all the nodes in that part in the dist array. For each node in that part, we find the no of nodes lying in other parts which are at prime distance , by iterating over all the primes and adding dist[Prime[j] – distance(i,centroid)] for each node i . Then again add the contributions of all the nodes in this part to dist and move on to the next part.
   • Since the contribution of each node to dist is added and removed only once, the overall complexity is O(N*P*logN) where P is the no of primes <=N .
   • Solution | CodeChef : see this for a better understanding if you are not yet clear 🙂
4. BST maintenance
   • Build the final BST in O(n) or O(nlogN) and do the centroid decomposition of that tree.
   • Initially all the nodes are inactive and we make them active one by one in their order of insertion. On making the i’th node active, we just need to compute the sum of distances of this node to the rest i-1 active nodes in the tree and add this sum to the answer of the first i-1 nodes.
   • Hence, for each node in the centroid tree we shall maintain three things,
     sum[i] = sum of distances of all the active nodes in the subtree (in centroid tree) of i till node i.
     contribution[i] = the contribution of all the active nodes in the subtree of i to sum[par[i]] , where par[i] denotes parent of node i in the centroid tree.
     cnt[i] = no of active nodes in the subtree of i.
   • Given the above information, On making node i active, the query would reduce to :
     sum[i] + (sum[par[x]]-contribution[x] + (cnt[par[x]] – cnt[x]) * dist(par[x],i) )  , for all ancestors x of i .
   • And each update would correspond to updating the values of the 3 quantities in each of the ancestors of node i in the centroid tree.
5. Other Problems (will be updated as and when found)
   • Page on ioi2011.or.th
   • Page on codechef.com
   • Page on codechef.com
   • SPOJ.com – Problem QTREE4
   • Problem – C – Codeforces [very basic application]
   • Solve Rasta in Tavaspolis
     
   • Problem – F – Codeforces
   • Contest Page | CodeChef

Conclusion

I hope that you now have a better understanding and feel of centroid decomposition. This blog was largely inspired by a discussion by Petr Mitrichev (competitive programmer) on Centroid Decomposition in his blog This week in competitive programming . This was the only resource I could find on the internet while learning Centroid Decomposition. He has also discussed a very interesting problem in his blog which I would suggest everyone to have a look on.

Comments and Feedbacks are most welcome.
Happy Coding 🙂

References :

• This week in competitive programming
• Page on cs.ubc.ca
• Page on mit.edu
• Centroid Decomposition of a tree – Codeforces
• Hackerrank problem BST maintenance – Codeforces

Note : Link to original post