Introduction : Well, don’t get too much carried away by the title of the blog. By the end of this article you shall realize the motivation behind it. 🙂
So, let’s begin :
Pre-requisites : Binary Search Tree and Binary Heap.
What is a Treap ?
Ans: In short, Treap is simply a Self-balancing binary search tree, but of course , much cooler 🙂 .
Why another BBT ?
Ans: Because , again , it’s much cooler . By that , i mean really easy to code (once you have a good understanding of course) and also, it can be extended to be used as not just a BBT but also other trees like interval trees (segment tree , fenwik tree) etc. In short, read on and you shall realize for yourself.
Introduction
Formal Definitions
- Cartesian Tree : A Cartesian Tree is just a binary tree on a sequence of pairs that is heap-ordered on one of the elements of each pair , and BST-ordered on the other element.
- Treap : In a Cartesian Tree, if we assign random values to each heap-ordered element , then the expected height of the resulting tree is O(logN). This is the entire idea behind Treaps.
Explanation
The above definitions might seem alien right now so do not worry and move on … 🙂
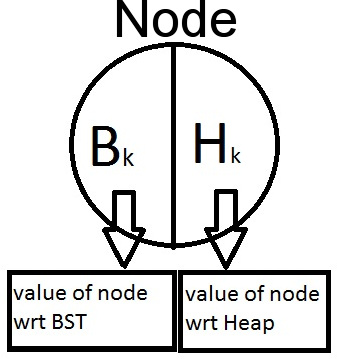
A Cartesian Tree is basically a tree in which each node stores a pair
(Bk,Hk) where
Bk => Corresponds to value of a node wrt BST
Hk => Corresponds to Priority of a node wrt Heap.
Thus, the position of a node in a cartesian tree would be decided by both it’s Bk and Hk values. The position of the node would be such that if the tree is traversed like a BST , the node would be represented by its Bk value and if the tree is traversed like a heap, the node would be represented by its Hk values. The Bk values of all nodes would maintain the BST invariant and Hk values would maintain the Heap invariant (min or max heap based on your choice).
Theorem-1 : Given a set of nodes i.e (Bk,Hk) pairs (with distinct H′ks), only a unique cartesian tree would exist for these nodes irrespective of their order of insertion
Proof : For a given set of nodes , the node with maximum priority would form the root of the cartesian tree . All the nodes with key less than(equal to) the Broot would lie in the left subtree of root and all the nodes with key greater than Broot will lie in the right subtree. Now inductively the left and right subtrees can be built.
Given the above definition of a Cartesian Tree , a Treap can now be defined as a Cartesian Tree in which, the Hk value of a node is assigned randomly from a large range of values (eg: by using rand() function in cpp) . This random assignment of Hk values helps maintain the height of the Treap approximately O(logN) . It is important to note that it is highly probabilistic that height of a Treap is O(logN) and not deterministic like other balanced BST’s like AVL , RED-BLACK etc. Although the height is approximately O(logN) , it gives sufficiently good results in practical scenarios and it is very difficult to get a worst-case O(n) .
Theorem-2: Random assignment of Hk values in a Cartesian Tree helps maintain the height of the tree to be approximately O(logN).
Proof: The mathematical proof of the above statement is beyond the scope of this article (see the original research paper in references for further details) .
To provide a basic intuition , we can imagine it as follows :
In a simple BST , the height of the BST depends upon the choice of the root . The closer the root lies to the median of the given data, the better would be the height of the resulting tree and assigning priority values randomly help us come closer to choosing a good root for each subtree i.e a worst-case O(n) height for a Treap would be achieved if for each subtree, the root node would lie towards the extreme end of the given data, which has a very less probability since the priorities are assigned randomly over a large range of continues data
Henceforth, in the whole article we shall assume the height of Treap to be O(logN) (Never forget the “approximately” part 🙂 )
The Real Stuff : Implementation
Treap supports two basic (and very powerful) operations : split and merge , both in O(H) where H is height of treap i.e O(logN) .
- split(T,X) : It splits a given treap T into two different treaps L and R such that L contains all the nodes with Bk<=X and R contains all the nodes with Bk>X . The original treap T is destroyed/doesn’t exist anymore after the split operation.
(The equality can be put on either side depending on your choice wlg. I prefer equality on the left side and so shall be used further in the blog) - merge(L,R) : The merge operation merges two given treaps L and R into a single treap T and L and R are destroyed after the operation. A very important assumption of the merge operation is that the largest value of L is less than the smallest value of R (where value refers to the Bk values of the particular node).Hence we observe that two treaps obtained after a split operation can always be merged to give back the original treap.
A cpp implementation of split and merge is as follows :
typedef struct node{
int val,prior,size;
struct node *l,*r;
}node;
typedef node* pnode;
int sz(pnode t){
return t?t->size:0;
}
void upd_sz(pnode t){
if(t)t->size = sz(t->l)+1+sz(t->r);
}
void split(pnode t,pnode &l,pnode &r,int key){
if(!t)l=r=NULL;
else if(t->val<=key)split(t->r,t->r,r,key),l=t;//elem=key comes in l
else split(t->l,l,t->l,key),r=t;
upd_sz(t);
}
void merge(pnode &t,pnode l,pnode r){
if(!l || !r)t=l?l:r;
else if(l->prior > r->prior)merge(l->r,l->r,r),t=l;
else merge(r->l,l,r->l),t=r;
upd_sz(t);
}
Explanation
- split :
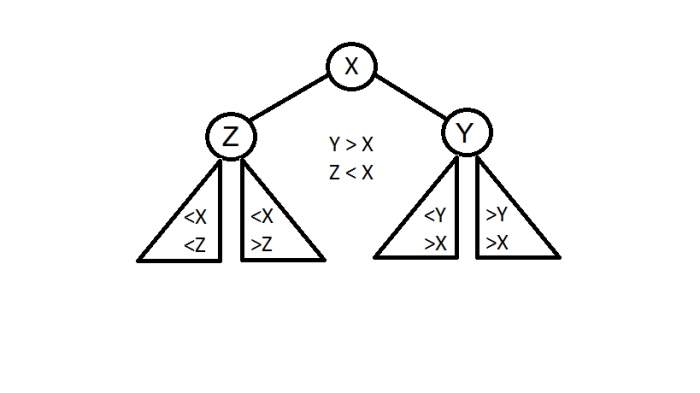
- if key >= X
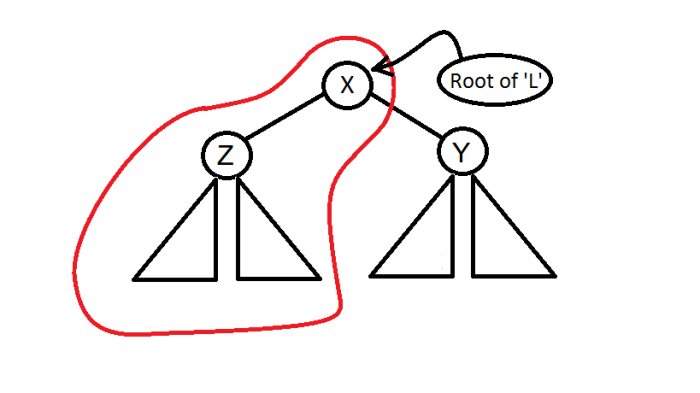
- Call the split function for Y and attach the root of L’ returned by this split as right child of X s.t. Treap invariant of ‘L’ is maintained (How?).
- L will still be heap ordered coz priority of all elements in Y is < X.
- L will still be BST ordered coz all elements in Y > X.
- Also, R of X = R’ returned by split on Y.
- else if key < X
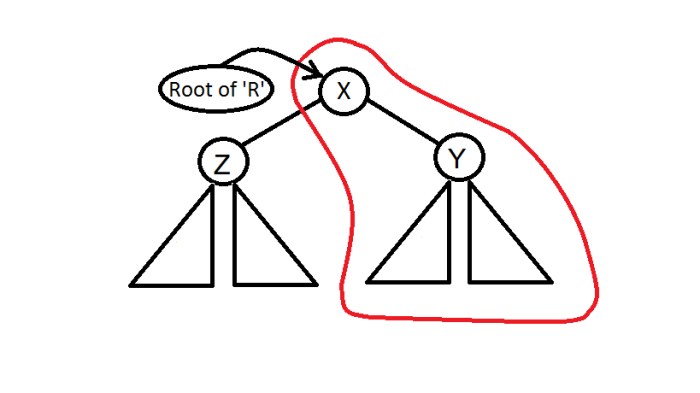
- Call the split function for Z and attach the root of R’ returned by split as left child of X s.t. treap invariant is maintained for ‘R’ (similar explanation as above).
- Also L for X = L’ returned by split of Z .
- if key >= X
- merge :
- How to choose the new root ? (assuming that we are following max-heap property)
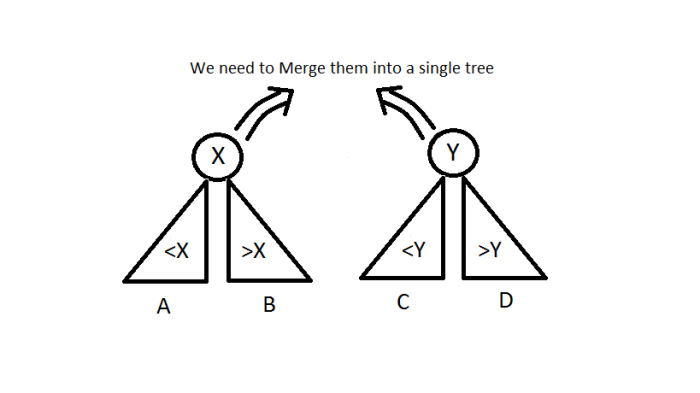
- if(priority(x) > priority(y))
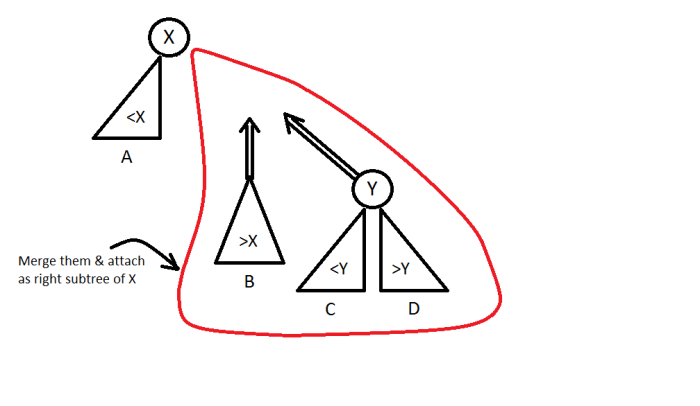
- else if(priority(y) > priority(x))
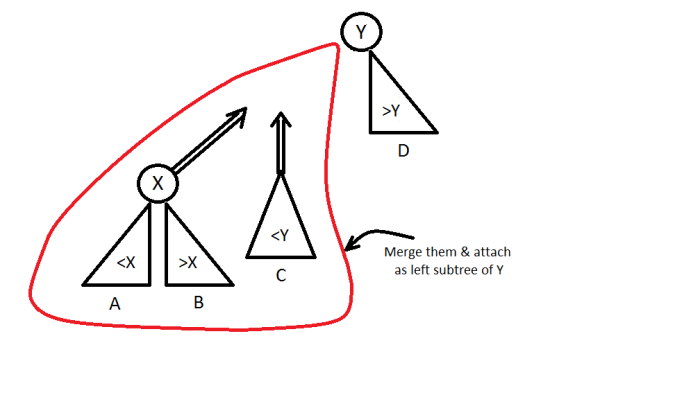
- if(priority(x) > priority(y))
- How to choose the new root ? (assuming that we are following max-heap property)
Operations of a BST :
Using the above split and merge operations , the operations of a BST like insert, find, erase etc. can be easily implemented.
- insert(X) : To insert a value X into our BST, we first chose a Y = rand() , such that (X,Y) represents the new node to be inserted in the treap. Then, keep on going down the tree like a simple BST searching for the correct pos where X should be inserted unless either the correct position is found OR we encounter the first node E s.t. priority(E) < Y . Here, call split(E,X) and attach L and R as left and right subtrees of node (X,Y) . (How does this work ? :O , if you are not sure then spend some time on what has been covered so far 🙂 )
- erase(X) : Go down the tree like a BST unless node to be deleted is found. If the node is found, call merge function for it’s left and right subtrees and attach the resulting tree to the parent of the node to be deleted.
- find(X) : same as simple BST.
See the following code for a clear understanding.
void insert(pnode &t,pnode it){
if(!t) t=it;
else if(it->prior>t->prior)split(t,it->l,it->r,it->val),t=it;
else insert(t->val<=it->val?t->r:t->l,it);
upd_sz(t);
}
void erase(pnode &t,int key){
if(!t)return;
else if(t->val==key){pnode temp=t;merge(t,t->l,t->r);free(temp);}
else erase(t->val<key?t->r:t->l,key);
upd_sz(t);
}
void unite (pnode &t,pnode l, pnode r) {
if (!l || !r) return void(t = l ? l : r);
if (l->prior < r->prior) swap (l, r);
pnode lt, rt;
split (r,lt, rt,l->val);
unite (l->l,l->l, lt);
unite (l->r,l->r, rt);
t=l;upd_sz(t);
}
pnode init(int val){
pnode ret = (pnode)malloc(sizeof(node));
ret->val=val;ret->size=1;ret->prior=rand();ret->l=ret->r=NULL;
return ret;
}
This covers the basic introduction to treaps and their implementation as Balanced Binary Search Trees. But there’s far more to treaps than just Balanced Binary Search Trees. For eg :
- A variant of treaps called Implicit Treaps can be used to perform all the operations which interval trees like segment tree and fenwick tree can (including lazy propagation :D) .
- Idea of sparse segment tree and sparse fenwick tree to handle very large ranges and limited queries can also be extended to treaps resulting in a variant called sparse implicit treaps.
- Treaps also make a good persistent BST mainly because of their simplicity to code and a constant average number of operations upon insert/delete.
- Treaps can also be extended to multiple dimensions in the form of quadtreaps which are a balanced variant of a quadtree data structure.
I would like to end this article here and in the next part i would cover some of the advanced applications of treaps mentioned above (mainly the first point i.e implicit treaps) .
Till then, happy coding 🙂
Practice Problems :
There are many applications/problems on BST. As a basic implementation practice of treap, try to get this accepted.
http://www.spoj.com/problems/ORDERSET/en/
References :
Original Research Paper : Page on washington.edu
Implementation Details : Декартово дерево (treap, дерамида)
Cartesian Trees vs Treaps : Treap – Codeforces
Note : Link to original post
HI,
Do you know a way to have the split function computed inplace (as it is now) but with the constraint that T is left unmodified?
Thank you,
LikeLike